Vertical mixing

import numpy as np
from datetime import datetime, timedelta
from opendrift.models.oceandrift import OceanDrift

Configuration. Edit this section to see the differences.

N = 10000  # Number of particles
seed_depth = -10 # meters
hours = 2  # Number of hours to mix particles
sea_floor_depth = 100  # m
timestep_seconds = 60  # Timestep for vertical mixing

terminal_velocity = 0  # Neutral particles
#terminal_velocity = 0.005  # Rising particles
#terminal_velocity = -0.005  # Sinking particles

# Profile of diffusivities
z = np.arange(0, -40, -1)

diffusivity = np.ones(z.shape)*.01  # Constant diffusivity
diffusivity[z<-20] = 0.001  # uncomment to reduce mixing below 20m

Preparing mixing timestep

time = datetime(2020, 1, 1, 0)
o = OceanDrift(loglevel=20)
o.set_config('drift:vertical_mixing', True)
o.set_config('vertical_mixing:diffusivitymodel', 'environment')
o.set_config('vertical_mixing:timestep', timestep_seconds)
o.set_config('environment:fallback:land_binary_mask', 0)
o.seed_elements(lon=4, lat=60, z=seed_depth, time=time, number=N, terminal_velocity=terminal_velocity)
o.time = time
o.time_step = timedelta(hours=hours)
o.release_elements()
o.environment = np.array(list(zip(np.ones(N)*sea_floor_depth, np.zeros(N))),
                dtype=[('sea_floor_depth_below_sea_level', np.float32),
                       ('sea_surface_height', np.float32)]).view(np.recarray)
o.environment.ocean_mixed_layer_thickness = np.ones(N)*50
o.environment_profiles = {
        'z': z,
        'ocean_vertical_diffusivity':
         np.tile(diffusivity, (N, 1)).T}

15:36:58 INFO    opendrift:509: OpenDriftSimulation initialised (version 1.14.0 / v1.14.0-6-gaedbab0)
15:36:58 INFO    opendrift.models.basemodel.environment:206: Adding a global landmask from GSHHG
15:37:02 INFO    opendrift.models.basemodel.environment:229: Fallback values will be used for the following variables which have no readers:
15:37:02 INFO    opendrift.models.basemodel.environment:232:    x_sea_water_velocity: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    y_sea_water_velocity: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    sea_surface_height: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    x_wind: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    y_wind: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    upward_sea_water_velocity: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    ocean_vertical_diffusivity: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    sea_surface_wave_significant_height: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    sea_surface_wave_stokes_drift_x_velocity: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    sea_surface_wave_stokes_drift_y_velocity: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    sea_surface_wave_period_at_variance_spectral_density_maximum: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    sea_surface_wave_mean_period_from_variance_spectral_density_second_frequency_moment: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    sea_surface_swell_wave_to_direction: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    sea_surface_swell_wave_peak_period_from_variance_spectral_density: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    sea_surface_swell_wave_significant_height: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    sea_surface_wind_wave_to_direction: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    sea_surface_wind_wave_mean_period: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    sea_surface_wind_wave_significant_height: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    surface_downward_x_stress: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    surface_downward_y_stress: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    turbulent_kinetic_energy: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    turbulent_generic_length_scale: 0.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    ocean_mixed_layer_thickness: 50.000000
15:37:02 INFO    opendrift.models.basemodel.environment:232:    sea_floor_depth_below_sea_level: 10000.000000

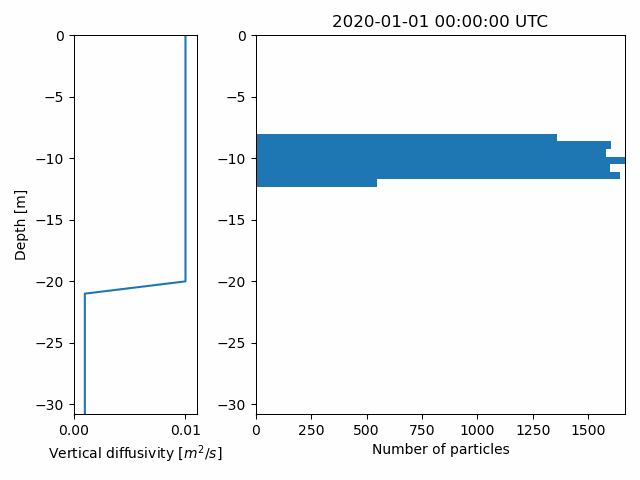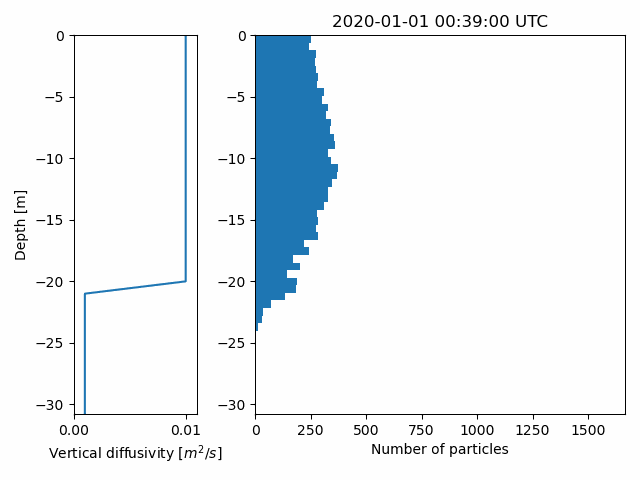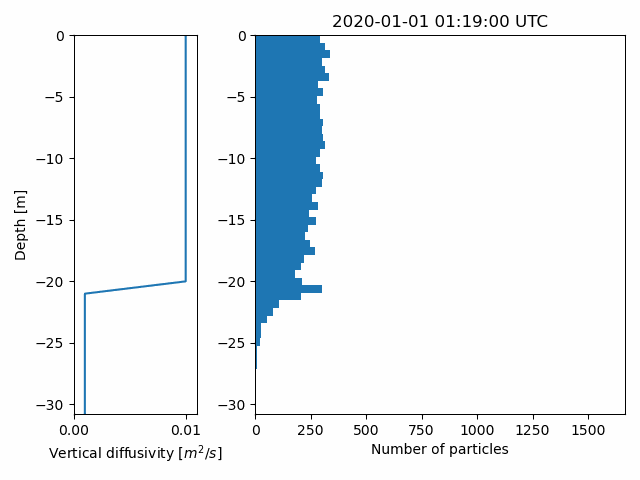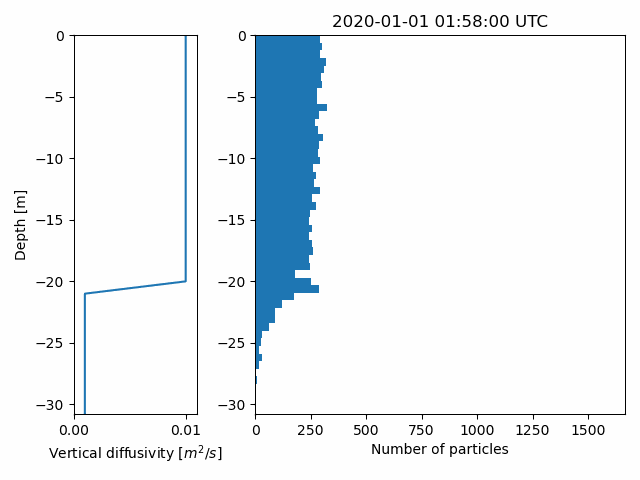
Calculate vertical mixing, and return particle depths at all positions

print('Calculating...')
depths = o.vertical_mixing(store_depths=True)

print('Making animation...')
o.animate_vertical_distribution(depths=depths)

Calculating...
Making animation...
15:37:03 INFO    opendrift:4650: Saving animation to /root/project/docs/source/gallery/animations/example_vertical_mixing_0.gif...
15:37:24 INFO    opendrift.models.oceandrift:629: Time to make animation: 0:00:21.657326